В. Г. Кон, НИЦ "Курчатовский Институт", Москва, http://kohnvict.narod.ru, 17-04-2011
Феномен Гиббса является частным случаем проблемы численного представления функции с резкими скачками через ее ряд фурье. Проблема состоит в том, что ряд Фурье очень медленно сходится и неизбежное обрезание ряда приводит к неустраняемым артефактам. Вот как это выглядит на примере функции
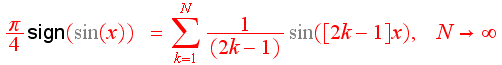
Ниже показаны графики этой функции для N = 5, 10, 20, 40, 80, 160
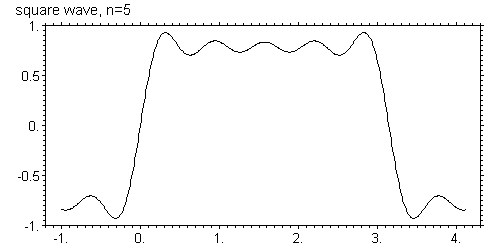
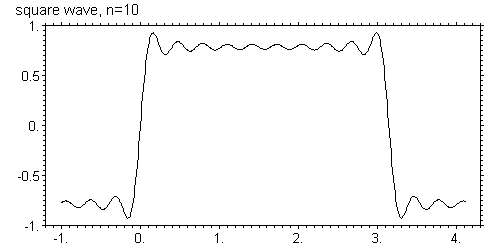
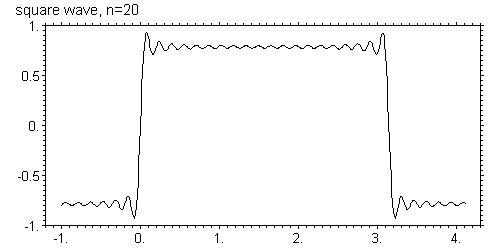
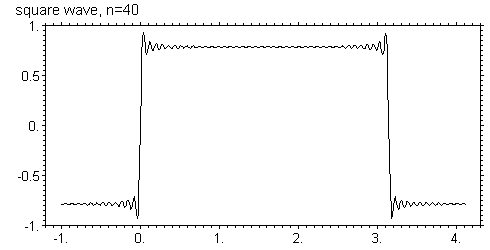
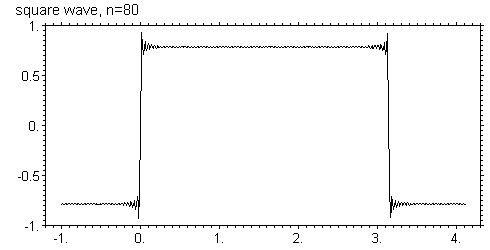
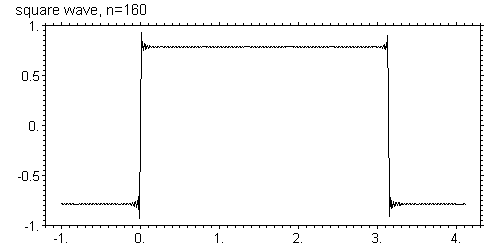
Видно, что с увеличением числа членов ряда он все более точно приближается к исходной функции в том смысле, что амплитуда осцилляций уменьшается, а частота увеличивается. Однако в узких областях вблизи скачков функции, отклонение все же остается. Более того, максимальное отклонение вообще не зависит от числа членов ряда и равно
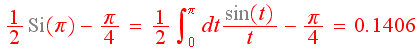
В этом собственно и состоит феномен, потому, что, с одной стороны, при увеличении числа членов ряда до бесконечности он должен абсолютно точно описывать функцию. С другой стороны, получается, что узкие области вблизи скачков нельзя описать ни при каком сколь угодно большом, но конечном значении N.
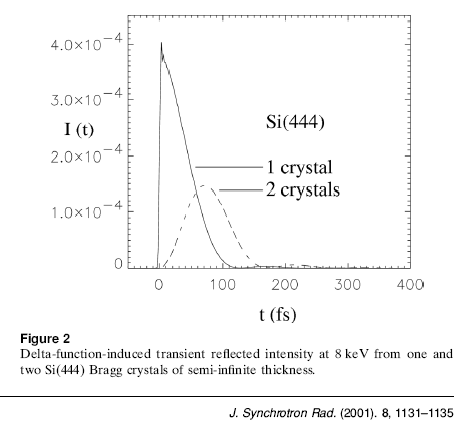Подобные артефакты встречаются для всех функций со скачками при численных расчетах функций по их преобразованию Фурье, если Фурье образ убывает обратно пропорционально волновому вектору (или члену ряда для периодической функции). Частным примером является функция Грина (пропагатор) для отражения рентгеновских лучей при дифракции по Брэггу в идеальном кристалле. Амплитуда отражения плоской волны зависит от волнового вектора или от частоты сложным образом, но при больших значениях (асимптотика) эта зависимость превращается в обратно пропорциональную. Результатом является резкий скачок отражения узкого пучка в точке его падения на кристалл или резкий скачок отражения мгновенной плоской волны, то есть пакета, сильно ограниченного во времени, в момент ее подхода к кристаллу. Но в численных расчетах этот скачок сопровождается осцилляциями Гиббса. К качестве примера справа показан график из научной статьи, опубликованной в 2001 году в журнале J. Synchrotron Rad. На нем виден резкий пик на максимуме кривой и осцилляции, представляющие собой феномен Гиббса. На самом деле максимум должен быть пологим, так как производная точной функции справа от скачка равна нулю.
Похожая, но несколько другая проблема возникает при расчете распространения рентгеновского излучения в воздухе методом пропагатора Киркгофа с использованием быстрого преобразования Фурье. В самой простейшей постановке задачи на оптический прибор падает плоская волна, для простоты будем считать, что она одномерная, то есть является функцией только одной поперечной координаты x. Эта волна комплексная. Оптический прибор изменяет как модуль, так и фазу комплексной волны. Пусть сразу после прибора она равна E(x,0). Ее распространение в воздухе вдоль оптической оси на расстояние z описывается сверткой E(x,0) с пропагатором Киркгофа P(x,z). В результате получается новая комплексная функция E(x,z), то есть
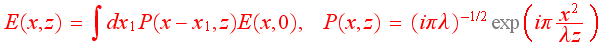
Здесь λ -- длина волны излучения. В пределе z = 0 пропагатор равен дельта-функции, а при малых значениях z он очень сильно осциллирует. По этой причине выполнить численный расчет в прямом пространстве весьма проблематично. Поступают по другому, а именно, учитывают свойство преобразования Фурье, согласно которому фурье-образ свертки равен произведению фурье образов сворачиваемых функций. Фурье-образ пропагатора Киркгофа легко вычисляется и тоже представляет собой функцию Гаусса, но теперь от волнового вектора q. Таким образом, необходимо численно вычислить фурье-образ исходной функции E(q,0) и умножить ее на фурье-образ пропагатора P(q,z), в результате получаем E(q,z) = P(q,z)E(q,0). После чего надо вычислить обратное преобразование Фурье для получения результата E(x,z) в прямом пространстве.
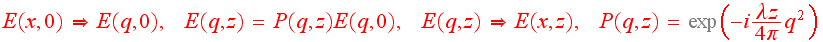
Одним из распространенных оптических приборов является зонная пластинка Френеля, которая скачком изменяет модуль и фазу падающей волны таким образом, чтобы в результате дифракции часть излучения сфокусировалась в малой области пространства. Главным параметром зонной пластинки является радиус первой зоны r1, который определяет границу первой зоны, отсчитывая ее из центра. Граница зоны с номером n определяются по формуле rn = r1n1/2. Соответственно фокусное расстояние зонной пластинки F = r12/λ. В результате самым сложным процессом оказывается вычисление прямого и обратного преобразований Фурье. Для этого существует численный метод быстрого преобразования Фурье (fast Fourier transformation или FFT), благодаря которому удается достаточно быстро решить очень большое число самых разных задач оптики. В простейшем варианте в этом методе задают систему точек с постоянным шагом в прямом пространстве с числом точек N = 2n, где n -- целое число. Если расчетная область равна X, то шаг сетки точек равен d1 = X/N. В обратном пространстве задают систему точек с тем же самым числом точек N и с шагом d2 = 2π/X. Таким образом, чем больше область в прямом пространстве, тем меньше шаг в обратном пространстве. Если необходимо иметь мелкий шаг как в прямом, так и в обратном пространстве, то приходится задавать очень большое число точек N. Функция задается только в области X, но предполагается что она периодическая с периодом X, поэтому необходимо, чтобы на краях интервала функция имела одно и то же значение, в частности она может быть равна нулю. Тогда в самом общем случае она описывается рядом Фурье с точно таким шагом, какой имеет наша сетка в обратном пространстве. Но, вообще говоря, этот ряд может быть бесконечным, а в нашем случае он имеет только N членов.
Чтобы показать cуть проблемы рассмотрим конкретный пример. Пусть область в прямом пространстве имеет размер X = 409.6 мкм, число точек N = 65536, длина волны излучения = 1 ангстрем. Рассмотрим зонную пластинку из золота с числом зон 20 и с диаметром апертуры 80 мкм. Толщина пластинки t = 2.674З мкм обеспечивает сдвиг фазы на π. За пределами апертуры пучок ограничен щелью, так что функция равна нулю. На рисунке показаны действительная и мнимая части комплексной волновой функции сразу за зонной пластинкой
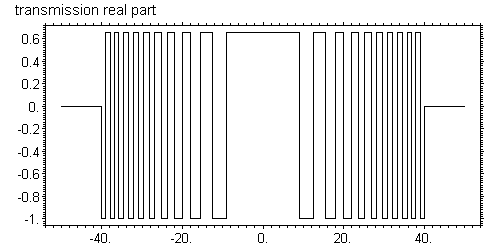
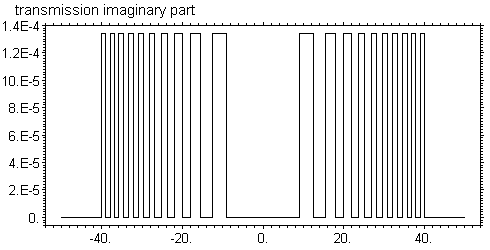
Заметим, что реально расчетная область больше, на рисунках показана только центральная часть, но за пределами апертуры функция равна нулю. Сдвиг фазы отсчитывается от центра, то есть фаза равна нулю в центре, хотя там есть материал и он поглощает. Это не совсем соответствует действительности, но известно, что постоянный сдвиг фазы не меняет распределение интенсивности, а это является главным результатом. Таким образом, фазу можно сдвинуть так, чтобы она была равна нулю в зонах с материалом, но модуль не равен нулю из-за поглощения. В пустых зонах, наоборот, нет поглощения, но фаза равна π. При этом мнимая часть очень мала и она не равна нулю просто потому, что сдвиг фазы не очень точно равен π. Используя метод FFT легко получить фурье-образ этой функции. Результат расчета показан на следующих рисунках
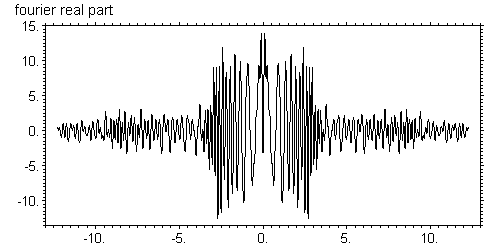
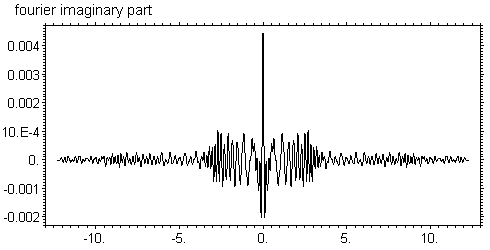
Здесь также мнимая часть очень мала. Реальная часть имеет две существенно различные области, центральную и хвосты. В обеих областях функция изменяется очень резко и достаточно сложным образом. Несмотря на это, если сделать обратное преобразование Фурье от этой функции, то мы получим исходное распределение с очень высокой точностью. Это означает, что точности математических расчетов вполне достаточно для того, чтобы получить полную воспроизводимость функции при двойном преобразовании Фурье. В чем тут фокус. Исходная математическая функция, заданная формулами, возможно имеет бесконечный ряд Фурье. Если его вычислять с конечным числом по точным формулам, то воспроизводимости возможно и не получить. Но я сначала получил численный массив в прямом пространстве на заданной системе точек, после чего численно вычислил фурье образ с использованием исходного численного массива. А метод FFT так устроен, что фактически прямое преобразование Фурье вычисляется умножением матрицы на вектор, а обратное -- умножением обратной матрицы на вектор. То есть двойное преобразование вычисляется умножением обратной матрицы на прямую, что дает единичную матрицу и исходную функцию с высокой точностью.
Ситуация резко меняется, как только попробовать выполнить расчет на некотором расстоянии от объекта. Фурье-образ пропагатора равен 1 независимо от q при z = 0, а при любом малом z больше нуля, он начинает медленно осциллировать. При этом центральная часть фурье-образа исходной функции не искажается, но длинные хвосты получают сдвиги по фазе. Очевидно следует ожидать сильного изменения волновой функции как раз около резких ступенек. Так оно и происходит. На следующих рисунках показано изменение волновой функции при z = 0.01 см.
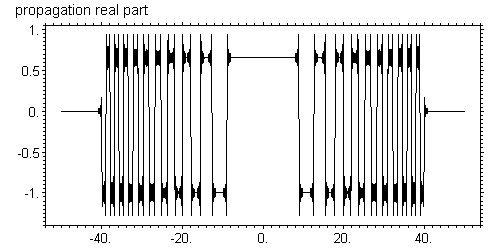
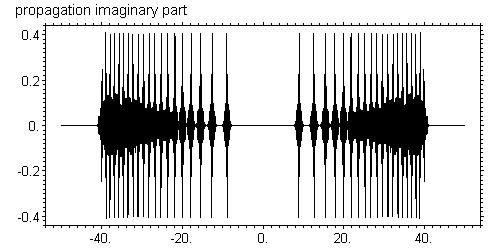
Интересно, что чем меньше зоны, тем сильнее они искажаются. Хотя характер искажения волновой функции похож на феномен Гиббса, но он имеет другую природу. В данном случае мы даже не знаем как должна вести себя правильная функция. Вполне возможно, что именно так она и должна себя вести. Действительно, в прямом пространстве пропагатор Киркгофа сильно осциллирует, а полный интеграл от него равен единице. Если исходная функция не меняется в какой-то области, то свертка с ней в этой области эквивалентна полному интегралу от пропагатора и результат снова не меняется. Дело в том, что интеграл от пропагатора набирается в конечной центральной области аргумента, а хвосты так быстро и равномерно осциллируют, что практически не дают вклада. Но если в какой то области исходная функция имеет резкую ступеньку, то это нарушает компенсацию в зонах пропагатора и осцилляции с мелким периодом вблизи резкой ступеньки фактически являются следствием осцилляций пропагатора. Чем дальше от ступеньки, чем меньше период осцилляций и меньше их амплитуда, так как происходит частичное усреднение. Таким образом, полученное поведение функции следует объяснять как супер-когерентность, которая приводит к интерференционным спеклам. Дело в том, что расчет проводится для полностью когерентного излучения, и он не соотвествует природе, потому что в реальности мы всегда имеем дело с частично когерентными источниками. Реальные источники находятся на близких расстояниях имеют вид расходящейся или сходящейся волны, причем существует много точек излучения, не согласованных по фазе. Более того, излучение представляет собой волновые пакеты, состоящие из многих длин волн. При регистрации излучения в течении длительного времени, разные частоты снова не согласованы по фазе. Наконец, сам детектор, регистрирующий излучение, имеет конечное разрешение по пространству. Интересно, что с ростом расстояния картина спеклов становится еще более сложной. На рисунках ниже показано распределение при z = 1 см.
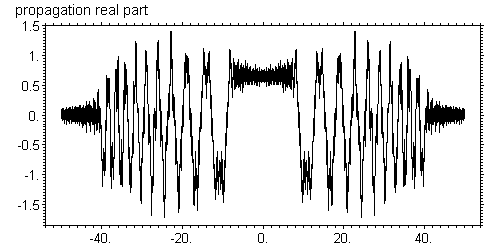
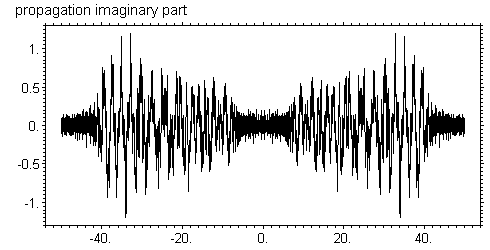
На первый взгляд может показаться, что такая картина обусловлена накоплением численных ошибок при расчете. Чтобы убедиться в том, что это не так, можно сделать расчет распространения излучения в обратную сторону, то есть на отрицательное расстояние. Очевидно, что пропагатор такого перехода соответствует отрицательном расстоянию и он просто комплексно сопряжен пропагатору для положительного расстояния. Я выполнил расчет по следующей схеме. Стартуя с исходной волновой функции сразу за зонной пластинкой я сделал переход на расстояние 1 см и затем обратный переход на такое же расстояние. Программа 4 раза выполняла преобразование Фурье. Результат расчета показан на рисунках
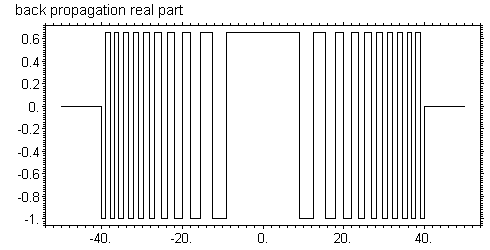
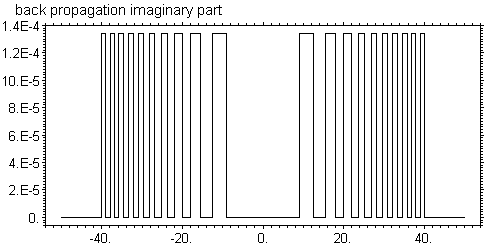
Таким образом, результат расчета с высокой точностью совпадает с исходной функцией. Это означает, по крайней мере, что при расчете преобразования Фурье ошибки не накапливаются. Означает ли это, что ошибок нет совсем. Ведь мы могли взять систему точек с любым шагом. И всегда прямой и обратный переходы будут давать исходную функцию, хотя характер осцилляций при расчете прямой функции может измениться. Прямого ответа на этот вопрос нет. Существуют способы точного расчета волнового поля для линейной зонной пластинки, не используя метод FFT. Было бы интересно сравнить результаты расчетов, выполненные двумя методами.
Есть еще один не вполне ясный вопрос. Шаг сетки в обратном пространстве равен d2 = 2π/X. Если фурье-образ волнового поля имеет длинные хвосты, то они должны правильно обрабатываться при умножении на фурье-образ пропагатора. Но последний очень сильно осциллирует на хвостах. При q = d2N/2, то есть на краю расчетной сетки, период осцилляций фурье-образа пропагатора равен dq = 4πd1/(λz). Существует расстояние, на котором половина периода будет равна шагу сетки d2. Это расстояние равно z = d1X/λ. Здесь нужно измерять d1 и X в микронах, длину волны в ангстремах и z в сантиметрах. Очевидно, что на этом и большем расстояниях пропагатор будет неправильно учитываться, так как его осцилляции не будут прописываться с нужной точностью.
Проблема не возникает, если хвосты фурье-образа волновой функции затухают на границах сетки. Если нет, то проблему можно решать двумя способами. Первый состоит в том, что нужно учесть, что исходно фурье-преобразование надо вычислять интегрированием, а не суммированием по сетке точек. Тогда можно ввести локальное интегрирование пропагатора по шагу сетки точек. В этом случае, если шаг сетки точек превышает период истинного пропагатора, то усредненный пропагатор начнет убывать по амплитуде. Я использовал такой прием, что позволяло значительно снизить амплитуду спеклов в области фокуса для зонной пластинки с большим числом зон. Однако, этот прием снижал максимальное значение интенсивности в фокусе по сравнению с точно известным. Другой способ -- просто сгладить исходную функцию подавляя ее высокие частоты, например, дополнительным умножением спектра на функцию Гаусса определенной ширины. Такой способ иногда полезен для получения более гладкой кривой без спеклов, но, вообще говоря, он не вполне законный. Гораздо проще убивать высокие частоты уже в результирующей интенсивности излучения тем же методом свертки с функцией Гаусса.
Тем не менее, нужно помнить вывод о том, что для больших расстояний z вычислять свертку методом двойного преобразования Фурье с использованием FFT не вполне корректно. Получается так, что при заданном шаге сетки в прямом пространстве нужно увеличивать размеры расчетной области, другими словами, увеличивать число точек сетки, независимо от размеров объекта. Этому есть причина, потому что дифракционная картина от малого объекта на больших расстояниях может быть значительно больше объекта. С другой стороны, если высокие частоты всего-то приводят к возникновению спеклов, то нет смысла стараться правильно их описать. А главная картина все равно определяется низкими частотами, для которых проблем нет.